Network Analysis of Partisanship
August, 2022
Over the last 230 years or so, the US Congress has met 117 times. In each of those sessions, hundreds to thousands of issues are put to vote. Certain issues are put to a "roll call vote", in which the votes of the individual members are collected and recorded. Those records still exist going back to the 1st Congress in 1789. The goal of this project is to use that data to measure partisanship and political polarization over time, first in the US Congress, but later in the US Supreme Court and in the German Bundestag (the bodies for which the data is most readily available).
The first step is to quantify partisanship.
The Vote Agreement Graph
Consider a graph where each vertex represents a Member of Congress. Now draw an edge between members each time they vote the same way on an issue. The resulting multigraph has hundreds of edges between members of the same party, and fewer edges between members of different parties. In the case of the current Congress (the 117th) graph looks something like this:
Let's call this the vote agreement graph. (The figure above shows a simplification of the vote agreement graph. The real vote agreement graph is a multigraph, and has edges between every pair of vertices because there have been unanimous votes.)
Even from this simple visualization, there are two clear communities in the 117th Congress, corresponding to the two major political parties. Compare this to the vote agreement graph for the 110th Congress:
The communities are still present in the 110th Congress, but they are not nearly as well defined as in the 117th Congress. Visually, there was more mixing in the 110th Congress, and the parties were not as divided.
These examples suggest that partisanship can be thought of as communities in the vote agreement graph, making it possible to measure the strength of partisanship by measuring the strength of community structure. This can be done using a concept from graph theory called modularity.
Modularity
Modularity is a standard measure of how well a given grouping of the vertices of a graph reflect the community structure of that graph. Essentially, modularity is higher when there are lots of edges between members of the same group, and lower when there are lots of edges crossing group lines.
Modularity is most often used as an objective function in community finding algorithms. Given a graph, if you can find a grouping that maximizes modularity, it is probably a good reflection of the communities in the graph. Such methods are common in analyzing social networks.
By measuring the modularity of the vote agreement graph using political parties as the groupings, it is possible to measure how "fuzzy" the political parties are, and consequently the strength of partisanship.
Using the examples above, the vote agreement graph for the 117th Congress has a partisan modularity of 0.39, while the same for the 110th Congress has a modularity of only 0.34, indicating less partisan voting.
Results in the US Congress
Computing modularity with data from Voteview, the plot below shows the modularity for each meeting of the US Congress from the 1st to the 117th:
Higher modularity corresponds to more partisanship, while lower modularity corresponds to less partisanship. A modularity of zero would mean there is no correlation between party affiliation and voting behavior.
There is a clear decline in partisanship from about 1900 until about 1970, after which there is a steady increase in partisanship until the present. The data before 1900 is quite noisy, with alternating periods of division and unity. For example, the 1820s show very low partisanship, while the 1840s show very high partisanship. While there are some differences, the House and the Senate generally follow each other closely.
Extending to the Supreme Court
The same methods can be used for any voting body where each member can be assigned some kind of party alignment. In the case of the US Supreme Court, justices have no party alignment. However, justices are often referred to as "liberal" or "conservative" based on the party of the president who nominated them. For the purposes of measuring modularity, the justices are assigned to parties based on the affiliation of the president who nominated them.
Computing modularity on the court using data from the Washington University Law Supreme Court Database gives this striking time series:
From 1791 until 2009, the Supreme Court shows modularity close to zero, indicating that the justices did not break into communities based on the political parties of their nominating presidents. (There are some small fluctuations, but I don't know enough about Supreme Court history to determine whether they are just noise.)
However, starting around 2009 and the appointment of Sonia Sotomayor, modularity shoots up:
I'll leave it to others to try to interpret these results. However, I should note this analysis only shows that, after 2009, Supreme Court justices tended to break into voting communities based on the party of their nominating presidents. It does not point to any particular mechanism, such as whether justices are influenced by partisan politics, or whether the selection process has become more partisan.
I should also mention that while the sudden jump in modularity is a break with historical precedent, modularity in the Supreme Court is still far less than that in Congress:
Note About Comparing Modularity Between Voting Bodies
In the plot above, the modularity of Congress is compared with the modularity of the Supreme Court. This can give a general idea of the strength of partisanship, but procedural differences could lead to biases in the results.
For example, votes in the US Congress are often done by voice, in which case no records are kept on the votes of individual members. Article. I. Section. 5. of the US Constitution says
[...] the Yeas and Nays of the Members of either House on any question shall, at the Desire of one fifth of those Present, be entered on the Journal.which means that the roll call vote is only recorded if one fifth of those present want it to be recorded. This selects for more controversial votes where the tallies might be close, or where a politician might want their vote to be recorded for posterity.
All of this means that procedural differences can lead to skewed results, either by only recording contentious votes, or by including non-contentious votes (like a "vote to start the session"). I will still do some inter-body comparisons, but they should be taken with a grain of salt.
The German Bundestag
Most voting bodies today have websites where anyone can see the results of recorded votes. However, the data on these official sites usually only goes back a few years. For some voting bodies, researchers have compiled long-term data by combing through old books and obscure government records. However, few voting bodies which have received such attention, restricting the subjects to which this modularity-based approach can be applied. (I couldn't even find good historical roll call data for the UK Parliament.)
One of the only easily available non-US datasets is BTVote, which includes roll call data from the German Bundestag (parliament) from 1949 to 2021. The Bundestag is a good case study both because the data is available, but also because it is a multi-party body, and an important feature of the modularity-based approach for measuring partisanship is that it works equally well in multi-party systems as in two-party systems.
Computed with data from BTVote, this shows the modularity of the Bundestag over time:
The result is somewhat noisy, but it shows that partisanship in the Bundestag generally increased from 1949 until about 1980, after which point it dropped sharply, and continued to steadily decrease until the present day. The plot below compares partisanship in the Bundestag to other voting bodies discussed above:
This shows that partisanship in the Bundestag has followed a unique curve over the last 70 years. However, as mentioned earlier, care should be taken when comparing the absolute modularity between voting bodies, as procedural differences can skew results.
Technical Notes
There are a couple technical details that I feel obligated to mention, but which do not fit into the broader narrative above. I've included them here in no particular order.
Comparison With Spatial Methods
There are a few existing methods which have been used to measure political polarization. Many work by assigning each member a position in some ideology space (for example, using DW-NOMINATE), and then measuring properties of the distribution of members (for example, how clustered are they? and how far apart are the clusters? etc.) The modularity based approach used here has several advantages over these spatial methods. Here are a few of them.
Multi-Party Systems
Spatial methods generally work by dimension reducing complex voting data to a few dimensions, which can then be interpreted as representing aspects of ideology. However, it isn't always clear how many dimensions are appropriate for the ideology space.
For example, modern US politics generally orients around a left-right spectrum, and so perhaps ideology space is one-dimensional. However, in other contexts, such as in some multi-party systems, more dimensions could be required.
This might be solvable by manually choosing the "correct" number of dimensions for each voting body (using some criteria for "correct"). However, ideology space has changed sufficiently over time that the correct number of dimensions today might not be the same as the correct number of dimensions 200 years ago. Maybe the US Congress is one-dimensional today, but maybe it wasn't in the 1820s. This leads into the next problem with spatial methods.
Changing Ideology Space
In most spatial methods, the positions of members in ideology space is computed by some kind of dimension reduction on roll call data. However, the structure of the resulting ideology space can be radically different from year-to-year. Though this is often solvable across short time frames (when there is little fundamental difference in ideology space), but presents a more fundamental problem across long time scales.
Here is an analogy. The figure below shows two spaces produced through dimension reduction. One is the dimension reduced space of images of animals (cats and dogs), while the other is the dimension reduced space of images of national flags:
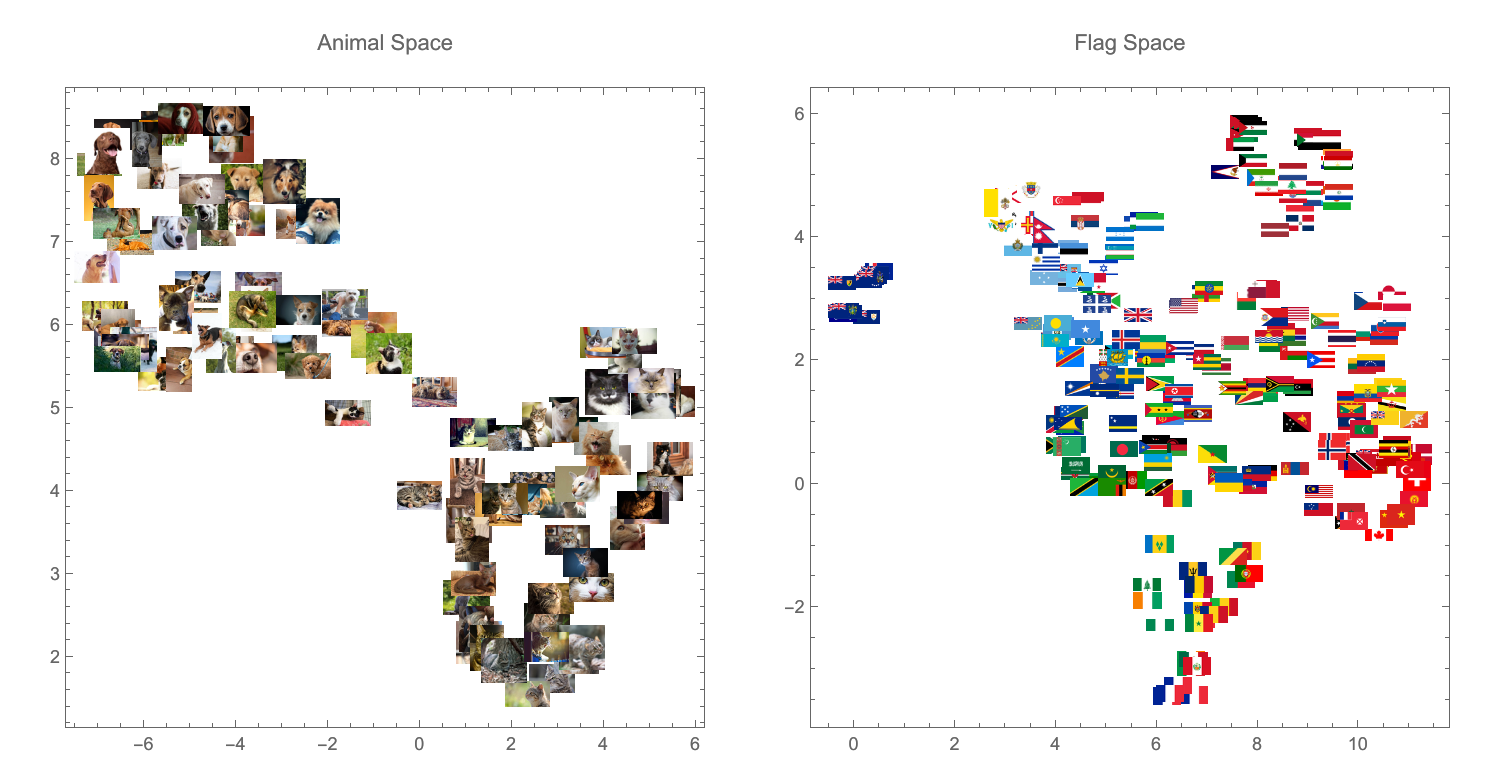
These two dimension reduced spaces are, in a sense, incomparable. There is no meaningful mapping from one to the other, and statistics on the distribution of points in animal space are incomparable with those from flag space.
For example, the distance of each point from the mean point could be measured in both of these spaces, but the resulting numbers would have nothing to do with one another, and comparing them would be meaningless. It would be like comparing joules and meters: it just doesn't mean anything.
Things get even worse if animal space and flag space don't even have the same number of dimensions. In this example, I've reduced both animal space and flag space to two dimensions. However, perhaps flag space would be most naturally represented in three dimensions, or four. Then comparing distances between points in animal space with distances between points in flag space would be even more meaningless.
If we were comparing "national flag space" with "city flag space", it might be possible to hack around these issues. The spaces would naturally be similar enough that it would probably be possible to construct them in a way that makes them roughly compatible. (This is essentially what D-NOMINATE does in the context of voting bodies.) However, these local fixes become impossible once the spaces are sufficiently different, as in the case of animal space and flag space.
Just as with animal space and flag space, the issues and ideologies of the 117th Congress (in 2022) could be so alien to those of the 17th Congress (from 1822) that comparing them would be fundamentally meaningless. The modularity-based approach used here sidesteps these issues by avoiding any kind of ideology space whatsoever.
What Is Partisanship?
Spatial methods assume that members correspond to positions in ideology space, and that they vote "yea" on issues that are close to their ideal point, and "no" on issues that are not. In this model, partisanship is a result of members moving further apart in ideology space.
However, some have argued that partisanship is driven by tribalism, not ideology. In a recent piece called The Myth of Ideological Polarization (available without subscription from the Internet Archive), Verlan and Hyrum Lewis argued
"Left" and "right" aren’t fixed and enduring philosophical belief systems. They’re merely social groups whose ideas, attitudes and issue positions constantly change. Since the meanings of "left" and "right" evolve, it makes little sense to speak of individuals, groups or parties moving "to the left" or "to the right."
In other words, political parties are more like social groups than positions in ideology space (at least according to the Lewises). Consequently, partisanship is a defined by tribalism and not ideological divergence.
In this model, ideology space based methods don't make much sense, as they only measure tribalism by proxy through ideology. However, the modularity-based model works even better.
Modularity is widely used to find communities in social networks, so applying modularity to vote agreement networks is a bit like measuring the strength of social communities in voting bodies, which gets to the core of partisanship under the tribal model.
Modularity Null Models
Modularity is computed by taking each pair of vertices \(u\) and \(v\) from the same group, and comparing the actual number of edges between \(u\) and \(v\) with a null model. Effectively, the null model is an estimate of the expected number of edges between \(u\) and \(v\) if the edges were distributed "randomly".
However, useful null models have to make assumptions. For example, the null model might have to preserve the degree distribution, or the total number of edges in the network, or some other metric.
In the standard formulation, the null model is an approximation of the configuration model with the expected number of edges between vertices \(u\) and \(v\) given by $$\frac{k_uk_v}{2m}$$ where \(k_i\) is the degree of vertex \(i\), and \(m\) is the total number of edges in the graph. I won't go into much detail about why this is the most common null model because plenty has been written by others on the subject.
The configuration model essentially represents a distribution of graphs which preserve the degree distribution. However, vote agreement graphs are not just any graphs. In particular, vote agreement graphs do not have self-loops. In large networks, the probability of self-loops in the configuration model limits to zero. However, in some of the very small networks used here (such as those for the Supreme Court, which has about nine vertices), the probability is much larger, leading to skewed results.
To solve this, a modified, a "no-loops" version of the configuration model can be used which disallows self-loops, as given by Cafieri et al. The resulting null model is $$\frac{k_uk_v}{2}\left(\frac{1}{2m-k_u} + \frac{1}{2m-k_v}\right)$$ Again, this no-loops null model limits to the standard null model for large graphs, but it gives different results for some of the smallest graphs used here. For example, this shows modularity over time in the Supreme Court using the standard and no-loops formulations of modularity:
Note that the standard formulation gives a negative modularity most of the time, which not only seems unintuitive, but actually makes no sense on further consideration. Using the no-loops formulation fixes these problems.
Code
A notebook with all code needed to reproduce this project is available here.
Data Sources
US Congress roll call data
Lewis, Jeffrey B., Keith Poole, Howard Rosenthal, Adam Boche, Aaron Rudkin, and Luke Sonnet (2022). Voteview: Congressional Roll-Call Votes Database. https://voteview.com/
US Supreme Court data
Harold J. Spaeth, Lee Epstein, Andrew D. Martin, Jeffrey A. Segal, Theodore J. Ruger, and Sara C. Benesh. 2020 Supreme Court Database, Version 2021 Release 01. URL: http://Supremecourtdatabase.org
German Bundestag roll call data
Bergmann, Henning; Bailer, Stefanie; Ohmura, Tamaki; Saalfeld, Thomas; Sieberer, Ulrich; Hohendorf, Lukas, 2018, "BTVote Voting Behavior", https://doi.org/10.7910/DVN/24U1FR, Harvard Dataverse, V2
Bergmann, Henning; Bailer, Stefanie; Ohmura, Tamaki; Saalfeld, Thomas; Sieberer, Ulrich; Hohendorf, Lukas, 2018, "BTVote MP Characteristics", https://doi.org/10.7910/DVN/QSFXLQ, Harvard Dataverse, V2
References
Cafieri, S., Hansen, P., & Liberti, L. (2010). Loops and multiple edges in modularity maximization of networks. Phys. Rev. E, 81, 046102. doi:10.1103/PhysRevE.81.046102