Functional Completeness and Optimization

November, 2016

(or Why the Apollo Guidance Computer Was Inefficient)

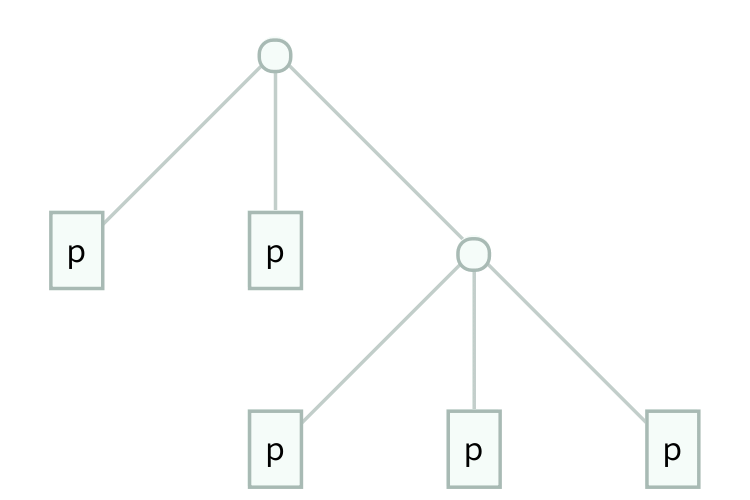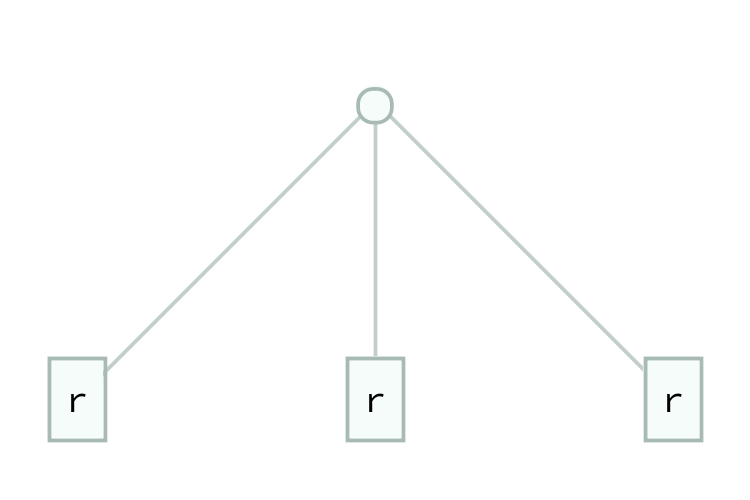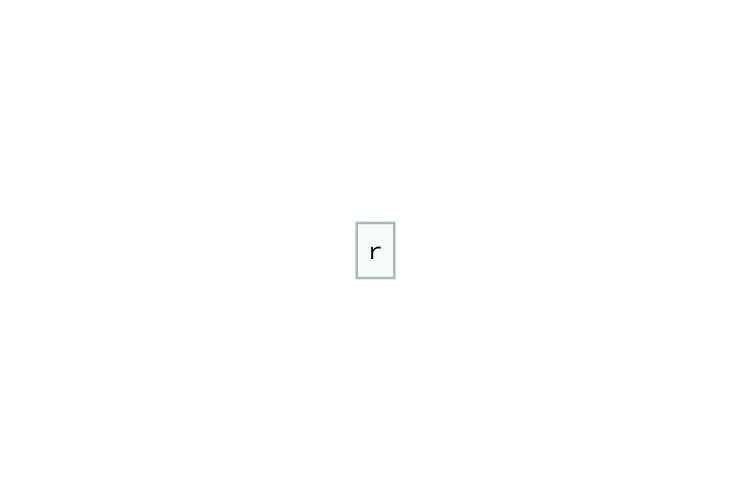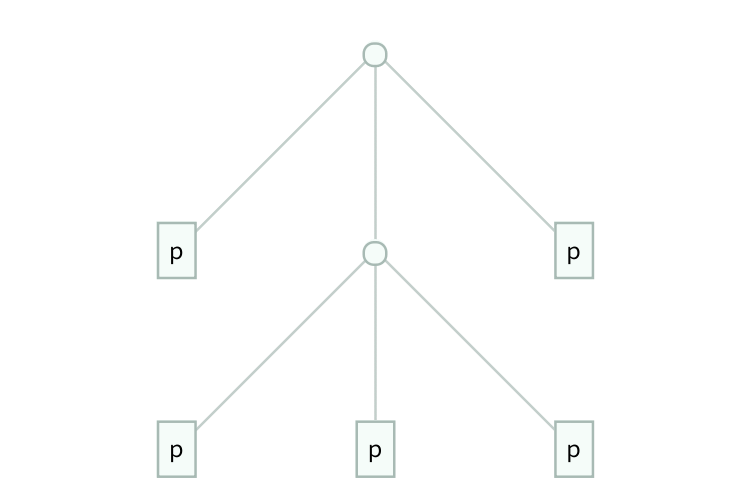
Background

A logical connective is a function which takes boolean values and returns a boolean value. AND, OR, and NAND are all examples of logical connectives. Sometimes, one logical connective can be written in terms of another. For example, OR can be written with NAND: $$\text{OR}(p,q) = \text{NAND}(\text{NAND}(p,p), \text{NAND}(q,q))$$ and XOR can be written with NOR: $$\text{XOR}(p,q) = \text{NOR}(\text{NOR}(\text{NOR}(p,p), \text{NOR}(q,q)), \text{NOR}(p,q))$$ Sometimes, however, this isn't possible. For example, there is no way to write NAND using only OR.

A connective \(f\) is functionally complete if all other connectives can be written with \(f\). Of the familiar 2-input connectives, only two are functionally complete: NAND and NOR. The functional completeness of NAND is the basis of virtually all semiconductors, as the behavior of a chip can be written in terms of logical connectives and it is easier to manufacture a chip using only a single logical connective.

3-Input Connectives

So far, I have only been talking about 2-input connectives like AND and XOR. However, these concepts can be generalized to 3-input connectives.

The question is, if you wanted to build a CPU with 3-input connectives, and you want to minimize the total number of gates, what connective should you choose? (This is not as theoretical as it might sound. The Apollo Guidance Computer used 3-input logic gates, and the Soviet Setun computer used 3-valued logic.) In order to answer this question, we need to know which 3-input connective can be used to write all other connectives using the fewest gates. That is, which connective \(f\) minimizes the total expression size of all the expressions of other connectives in terms of \(f\)?

This problem is simple in the 2-input case because the numbers are small enough that everything can be solved by brute force. For example, it is easy to find the minimal expression for writing OR in terms of NAND just by trying all possible expressions until you find one that works. However, the number of expressions that need to be considered grows so quickly that brute force is impossible for the 3-input case.

I designed and implemented a dynamic program in C++ which takes a 3-input connective \(f\) and finds the minimal expressions for writing all other 3-input connectives in terms of \(f\), as long as it is possible. I'm not going to write too much about the details of the algorithm, but feel free to contact me if you are interested. Using my dynamic program, I found that the connective with the following truth table was the most efficient: $$ \begin{array}{c c c | c} p & q & r & f(p,q,r) \\ \hline T & T & T & F \\ T & T & F & F \\ T & F & T & F \\ T & F & F & T \\ F & T & T & T \\ F & T & F & F \\ F & F & T & T \\ F & F & F & T \end{array} $$ Here are the expressions for representing \(g(p,q,r)\) in terms of this connective \(f\), for every one of the 256, 3-input connectives \(g\):

This connective minimizes the total leaf count of those expressions. (I should also mention that there are 6 connectives tied for first place, but they are all equivalent by symmetry.) The animation at the top of the page is a representation of these expressions. My program can also minimize the total depth, but I will focus on leaf count here.

As mentioned above, the Apollo Guidance Computer used 3-input logic gates. In particular, it used a generalized version of NOR. As you can see looking at the truth table above, NOR is not the most efficient choice, and in fact, it is actually tied for the least efficient choice! The total leaf count of the most efficient connective is 647, while the total leaf count with NOR is 1643.

A Note About the Number of Functionally Complete Connectives

While working on this project, I also wondered about the number of functionally-complete connectives. It turns out that this can be found relatively easily, and the authors of this paper computed that the number of functionally complete \(n\)-input connectives is \(2^{2^n-2}-2^{2^{n-1}-1}\). That might seem like a lot, but there are \(2^{2^n}\) connectives, so the fraction of \(n\)-input connectives which are functionally complete is $$\frac{2^{2^n-2}-2^{2^{n-1}-1}}{2^{2^n}} = \frac{1}{4} - \frac{1}{2^{1+2^{n-1}}}$$ which very quickly limits to \(\frac{1}{4}\) as \(n\) goes to \(\infty\) (all of which I computed with Mathematica).